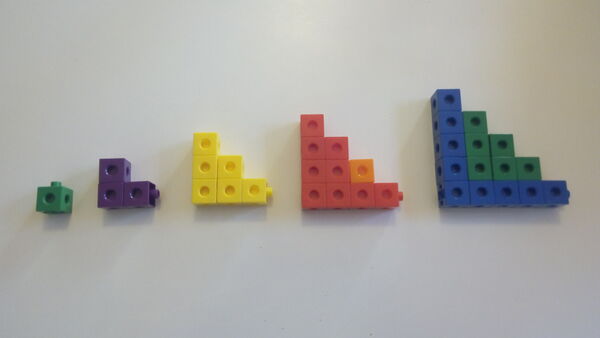Comencem la classe mostrant la primera imatge. Repartim els policubs en grups de quatre i demanem que la construeixin amb els policubs i que n'afegeixen uns quants.
Un cop n'han afegit uns quants, els hi demanem que els numerin, començant per l'1, per saber la posició i que diguin quants policubs caldrien per fer el que estaria a la posició 10. I el que estaria la posició 25? i a la 100?
Demanem que escriguin una expressió que pugui explicar el que passaria per qualsevol cas. Que ho expressin com més els hi convingui. Ho escriu cadascú a la seva llibreta, ho comenten en parella i després decideixen una expressió per grup. Escrivim a la pissarra les propostes de cada grup.
Sabries dir a quina posició es necesssiten exactament 17 policubs? I 193? I 8127?
Continuem amb la següent imatge
Demanem el mateix. Que reconstrueixin la imatge i que la continuïn. Que cerquin quants policubs necessitarien per la posició 10, 25 i 100. En tenim prou amb els policubs que tenim a classe? Quantes vegades els que tenim a classe, necessitaríem?
Tornem a demanar que escriguin l'expressió. Primer cada persona sola, després en parella que en consensuin una i finalment per grup. Ho comentem en gran grup.
Ens sabries dir a quina posició necessitaríem exactament 121 policubs? I 256? I 900?
Ho posem una mica més difícil. Ara treballem amb els nombres triangulars i fem el mateix per la imatge següent:
Demanem les mateixes coses: reconstrucció de la imatge, càlcul de les següents, nombre de policubs necessaris per la posició 10, 25 i 100, i finalment, l'expressió que representa qualsevol nombres de policubs.
Aquest cop, l'expressió se'ns complica una mica més i ens cal provar diferents opcions per trobar l'expressió.
Primer de tot, ens podem fixar en que els nombres triangulars són la suma dels nombres des de l'1 fins a l'actual.
| 1 | 1 |
| 2 | 1+2=3 |
| 3 | 1+2+3=6 |
| 4 | 1+2+3+4=10 |
| 5 | 1+2+3+4+5=15 |
Per tant, si deduïm quina és l'expressió, podrem saber quina és la suma de tots els nombres anteriors a un nombre donat. És a dir, si escollim el nombre 20, podrem saber quina és la suma de tots els nombres anteriors a 20, és a dir, 1+2+3+4+..+19+20.
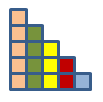
La manera més senzilla per trobar l'expressió és fer-ho de forma geomètrica. Si agafem qualsevol element i l'ajuntem amb el seu anterior girat, observem que formen un rectangle. A partir d'aquest rectangle, podem saber quants elements necessita cada vegada. O dit d'una altra manera, si agafem cada element i li sumem ell mateix girat, obtenim que per la posició 5 tenim el següent rectangle de 5*(5+1) per la posició 5.
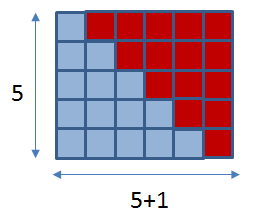
A veure com ho faries? Et serveix d'alguna informació aquesta pista?
Si t'hi fixes, si agafem l'expressió del rectangle, seria n*(n+1), però com que necessitem exactament la meitat dels policubs del rectangle, ens cal agafar l'expressió i dividir-la per dos. Per tant, a la posició n, necessitem n*(n+1)/2 policubs. Funciona? Comprovar-ho!
Ara preguntem, a quina posició es necessitarien exactament 36 policubs? Per poder-ho saber, ens caldria trobar el valor de n pel qual n*(n+1)/2=36. Per això ens cal resoldre l'equació, només cal passar el dos multiplicant a l'altre costat: n*(n+1)=72 i cal trobar un nombre que multiplicat pel següent ens dongui 72. El pots trobar? 6*7=42, 7*8=56, 8*9=72!!! Per tant, n=8.
Sabries trobar a quina posició necessitaríem exactament 91 policubs? I 7626?
Ara podem recuperar el que hem dit abans, que amb aquesta expressió podem calcular quina és la suma dels nombres anteriors a un nombre donat. I si volem saber la suma dels nombres anteriors a 20, només ens cal multiplicar 20*21/2=10*21=210. En aquest punt podem introduir l'anècdota de Gauss que va tenir quan tenia 7 anys a l'escola, quanel professor va demanar que calculéssin la suma dels primers nombres i en Gaus ho va resoldre de forma molt ràpida utilitzant un altre truc: Anècdota de Gauss i la suma d'1 a 100.
Finalment, acabem amb una de les activitats més riques i boniques que podem trobar a l'ARC.
Ara ens cal repetir el mateix procés, però aquest cop amb aquesta torre.
Aquest article és una adptació del més extens article de la campanya de Laboratoris del CESIRE, una activitat de l'ARC i una d'orientacions practiques per la millora de la Geometria.