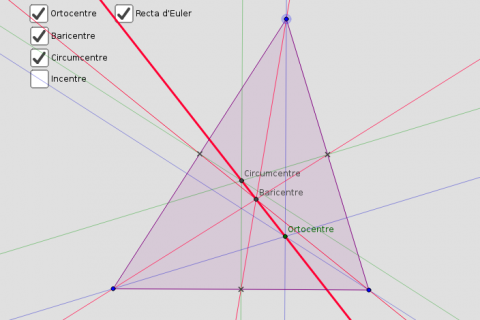
En aquesta activitat demostrarem l'existència de la Recta d'Euler:
L'ortocentre, el circumcentre i el baricentre d'un triangle són colineals.
L'ortocentre ve donat per la intersecció de les tres altures d'un triangle, el circumcentre per la intersecció de les tres mediatrius i el baricentre com la intersecció de les tres mitjanes.
En aquest activitat, creada mitjançant el Geogebra, construirem la Recta d'Euler seguint els següents passos.
- Contruim un triangle, que no cal que sigui polígon regular.
- Calculem els tres punts intermitjos de cada aresta entre els vèrtexs.
- Dibuixem les tres rectes que van entre un vèrtex i el punt intermig del costat contrari, s'anomenen mitjanes.
- Calculem el punt d'intersecció de les tres rectes: S'anomena baricentre. Canviarem la mida i el color del punt per distingir-lo dels altres.
- Dibuixem les tres altures: Recta ortogonal a una aresta que passa pel vèrtex contrari.
- Calculem el punt d'intersecció de les tres altures: ortocentre. També canviarem la mida i el color per destacar-lo.
- Finalment, dibuixem les tres rectes que són ortogonals a una aresta i que passa pel punt mig de la mateixa aresta, mediatriu.
- Busquem el punt d'intersecció de les tres rectes: S'anomena circumcentre. Altre cop, canviarem la mida i el color.
- La recta d'Euler es construeix demostrant que els tres centres (ortocentre, circumcentre i baricentre), estan alineats, és a dir, estant a la mateixa línia.
- Demostra-ho movent els vèrtexs i veient que encara que movem el triangle, els tres centres estan alineats.
Curs:
Tipus de node:
Contingut:
Duració:
1
Metodologia:
Distribució dels alumnes: