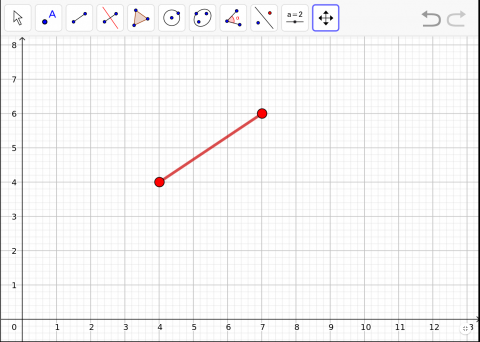
Aquesta activitat s'ha de fer en Geogebra.
Es mostra un segment que vagi de la coordenada (4,4) cap a la (7,6) de manera que tenim un costat d'un triangle igual que el vector (3,2).
La pregunta és: Quins triangles isòsceles puc crear diferents comptant que aquest és un dels costats del triangle? La única condició és que els vèrtexs del triangle han de caure sobre coordenades enteres.
Tenim tres possibilitats:
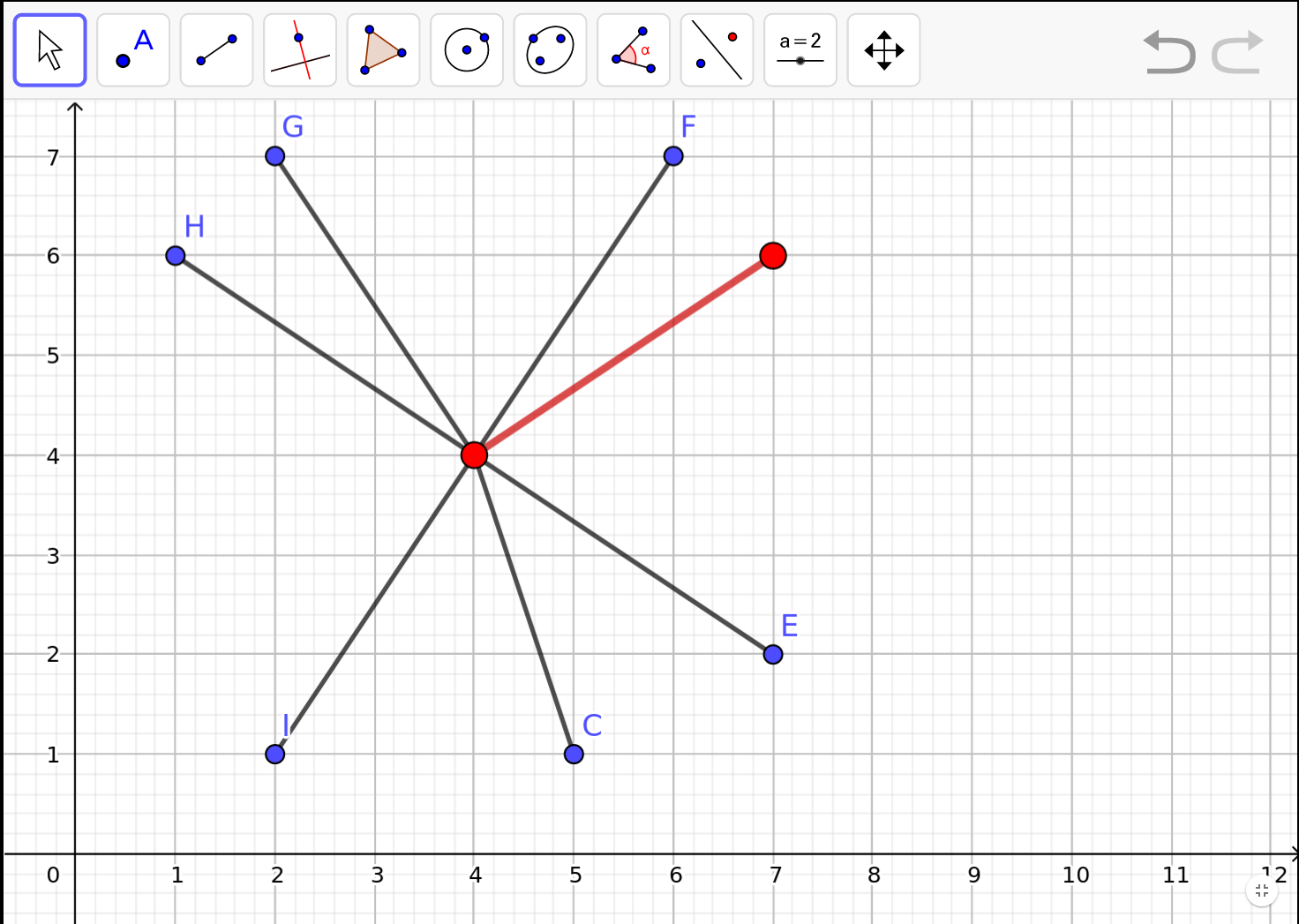
- El costat que tenim és un dels dos costats iguals i tots dos costats iguals coincideixen en el vèrtex (4,4)
- El costat que tenim és un dels dos costats iguals i tots dos costats iguals coincideixen en el vèrtex (7,6)
- El costat que tenim és el costat diferent.
Pel primer cas dibuixarem les següents possibilitats:
Per segon cas, les mateixes però a l'altra banda:
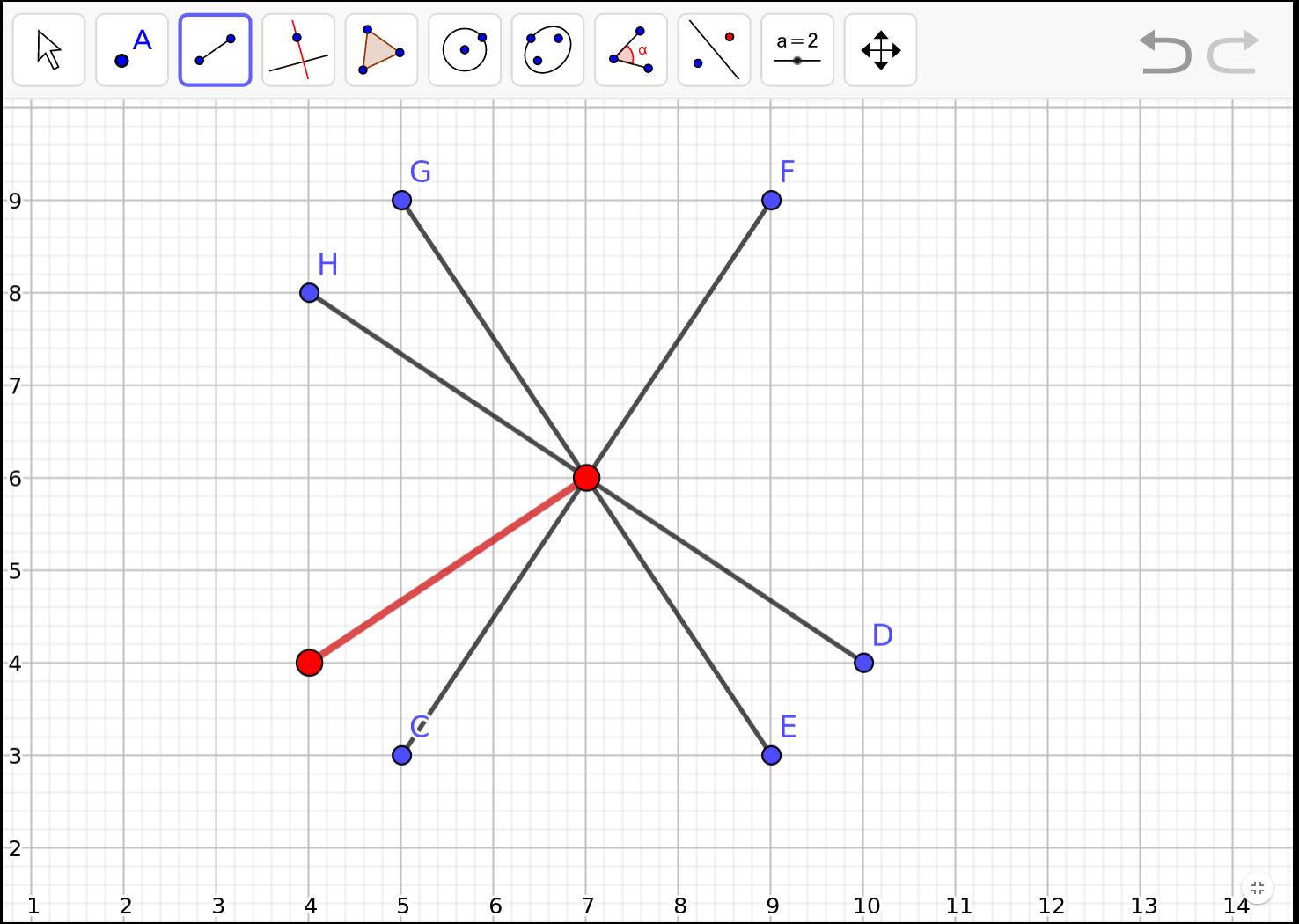
Per tant, tenim 6 possibilitats per cada banda. De fet, hauriem de construir la circumferència de centre un dels vèrtexs i radi fins a l'altre vèrtex. D'aquesta manera, qualsevol punt de la circumferència ens permet construir triangles isòsceles diferents. I veurem totes les possibilitats de costat que hi ha amb vèrtexs enters.
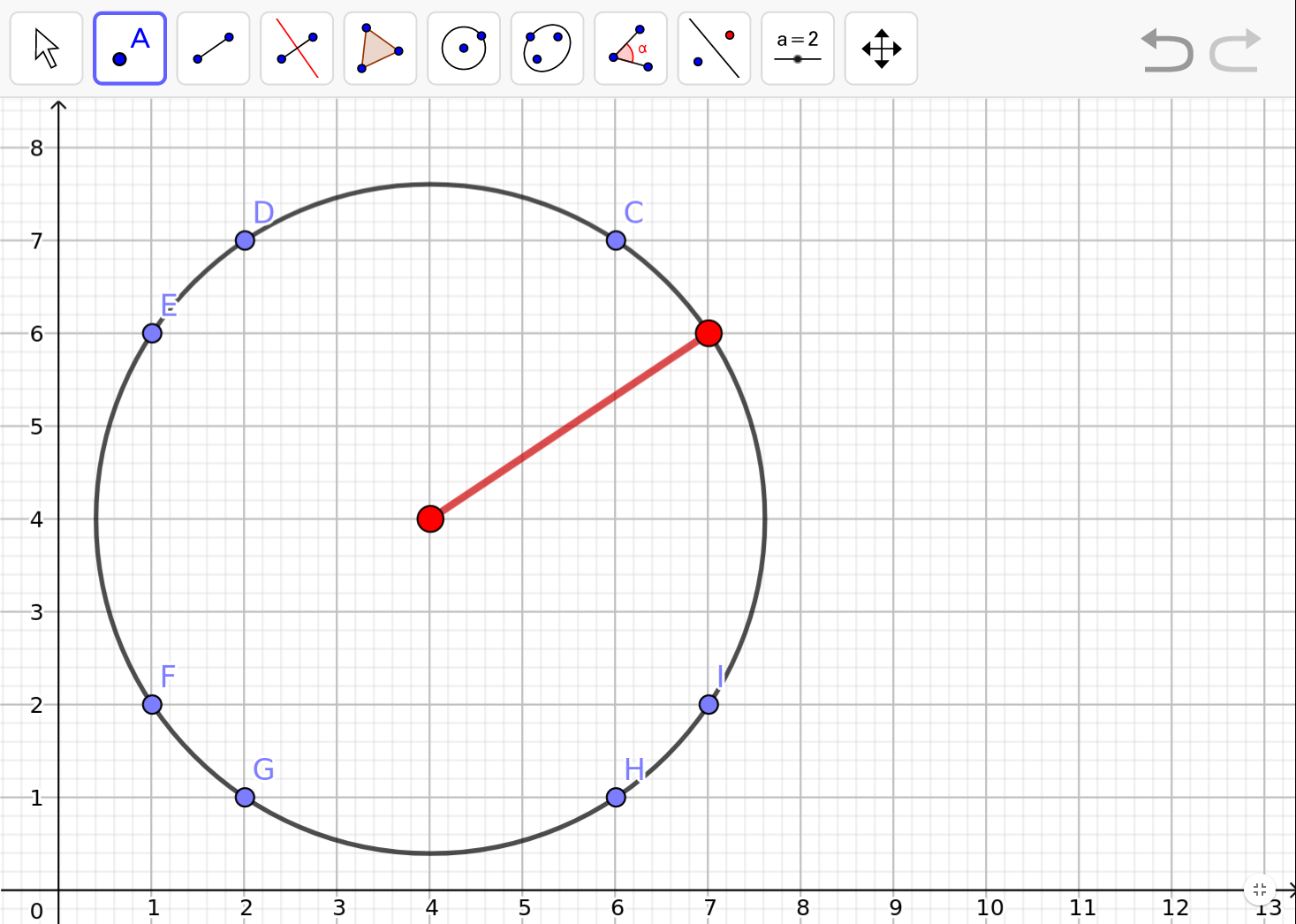
Que podeu comprovar el punt F també seria un possible punt pel triangle, és a dir, el punt (1,2), però no pot ser perquè no seria un triangle, serien dos segments units com un de sol o, dit d'una altra manera, l'angle entre els dos costats iguals hauria de ser 0, per això el descartem.
Si ara ens enfrontem al 3r cas, veurem que busquem punts que estiguin a igual distància dels dos extrems del segment. Per tant, estem buscant el lloc geomètric dels punts que equidisten dels dos extrems. Això, per definició, és la mediatriu entre els dos punts. La construïm:
I si cliquem a l'eina mediatriu i després cliquem als dos punts, obtenim el següent:
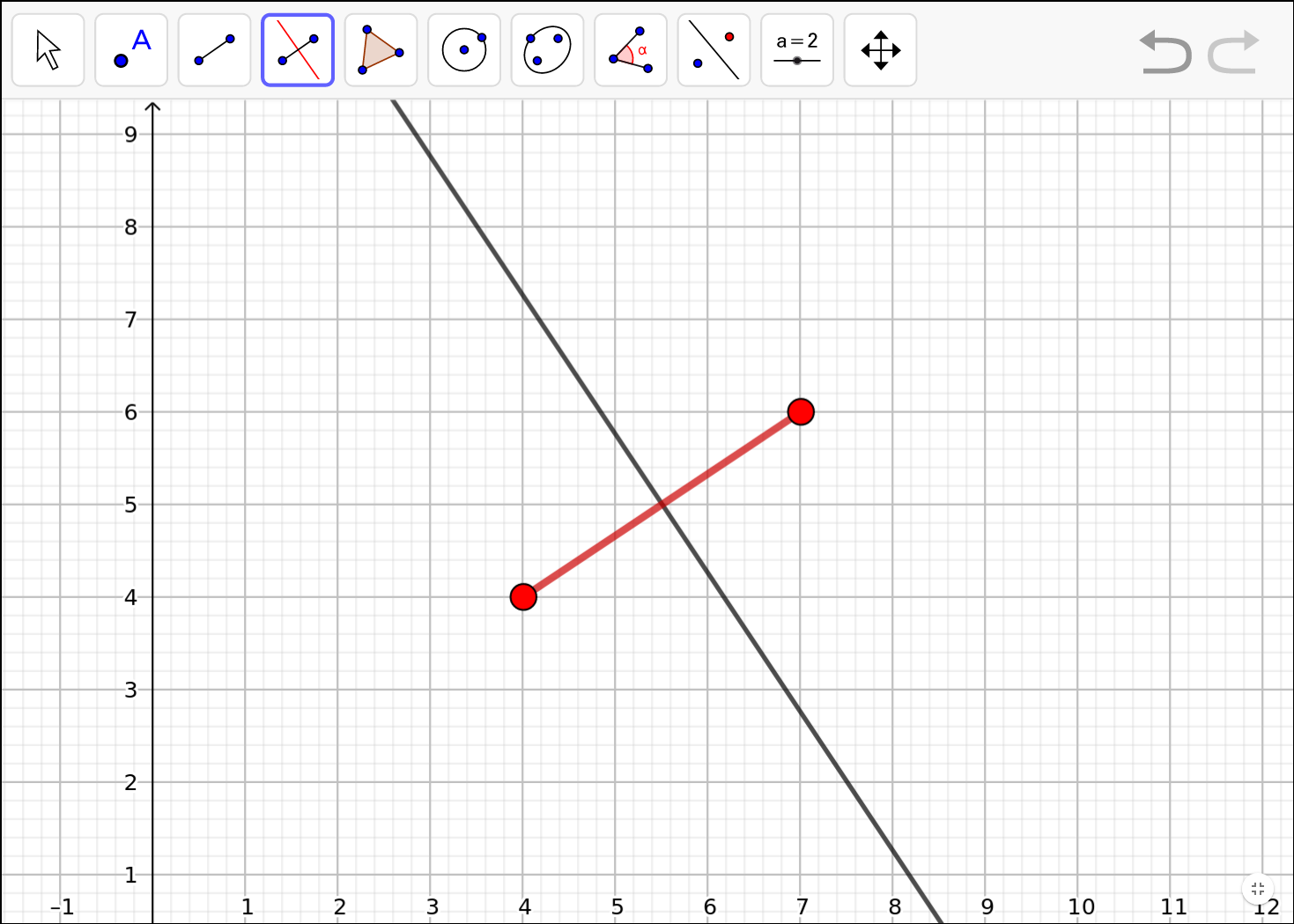
Si ara cliquem a sobre de qualsevol punt de la mediatriu, obtenim el 3r vèrtex d'un triangle isosceles, per tant, en tenim infinits:
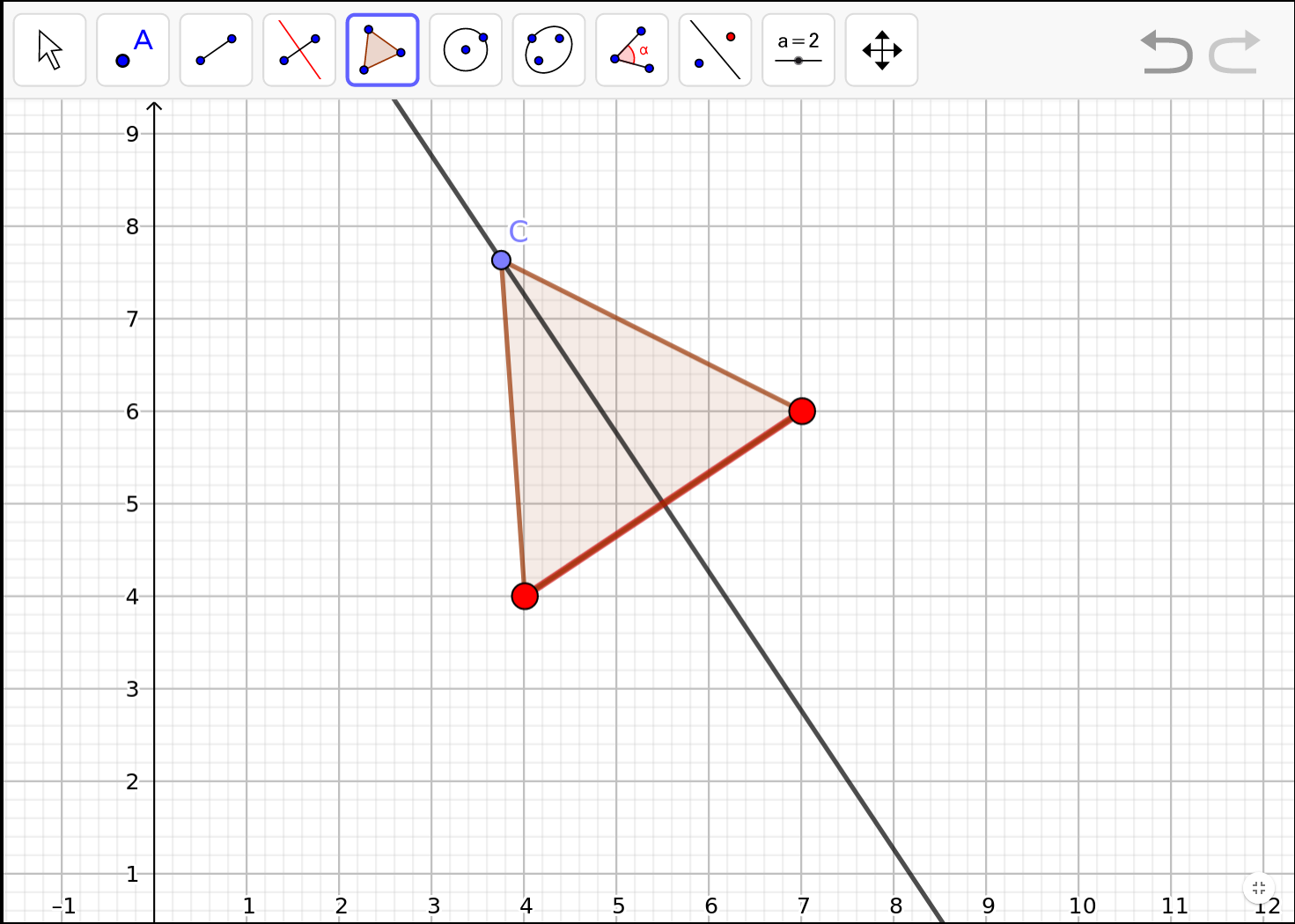
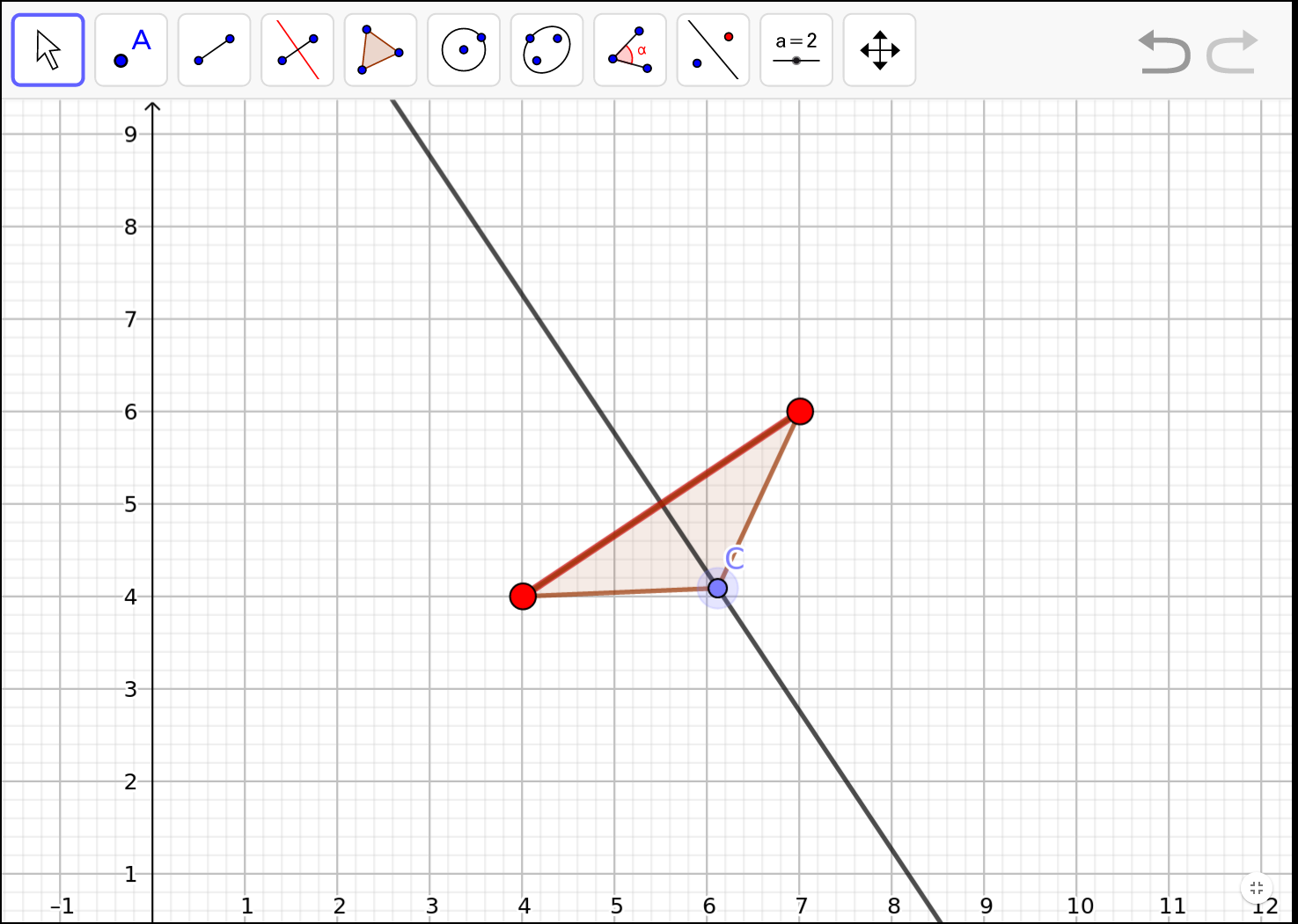
Però cal que el 3r vèrtex caigui sobre coordenades enteres. N'hi cau algun?
A simple vista sembla que no, però caldria demostrar-ho. Per això escriurem la recta de la mediatriu.
Tenim que passa pel punt mig dels dos vèrtexs, el qual el trobem sumant els punts i dividint per dos. Si considerem que V1 és el primer vèrtex i V2 és el segon:
(V1+V2)/2=((4,4)+(7,6))/2=(11/2,5). També sabem el vector ortogonal a la recta, que podem agafar justament el vector que defineix el segment, el (3,2).
D'aquesta manera podem esciure l'equació general de la recta Ax+By+C=0 sabent que (A,B) és el vector ortogonal a la recta d'aquesta manera:
3x+2y+C=0, sabent que passa pel punt (11/2,5), llavors 3*(11/2)+2*5+C=0, per tant, 33/2+10+C=0, 53/2+C=0, C=-53/2. Per tant l'equació de la nostra recta és:
3x+2y-53/2=0. Si en traiem els denominadors obtenim la següent equació diofàntica: 6x+4y=53.
I ara ens preguntem, existeixen algun parell de nombres enters (x,y) de manera que compleixen l'equació?
Ara ens tocaria explorar diferents nombres i anar comprovant a veure si podem trobar nombres que ho compleixin.
Es pot provar d'aïllar una variable respecte a l'altra i viceversa, provar valors ...
Però si ens aprofitem del que sabem de les equacions diofàntiques de la wikipedia:
Una condició necessària i suficient per què amb enters, tingui solució, és que el màxim comú divisor d' i divideixi a .
Per tant, en el nostre cas, mcd(6,4)=2 i 2 no divideix a 53. Per tant, no té solucions enteres, i per tant, no hi ha cap més triangle isòsceles possible.
Si canviem de posició el segment donat al principi del problema, canvien les solucions? N'hi ha més? De què depèn?